penyajian data dengan Histogram, Poligon dan Pie (lingkaran)

Langkah menyusun tabel distribusi frekuensi

1.     Mengurutkan data dari yang terkecil ke yang terbesar

2.    Menentukan daerah jangkauan (range) = R

3.    Menentukan banyaknya kelas/kelompok dengan menggunakan aturan Sturgess yaitu: k = 1 + 3,3 log n , n = banyaknya datum

4.    Menentukan interval kelas: I = R / k

5.    Menentukan batas kelas yaitu batas atas dan batas bawah

6.    Menentukan tepi kelas

          1.             Tepi atas kelas = batas atas kelas + 0,5

          2.            Tepi bawah kelas = batas bawah kelas – 0,5

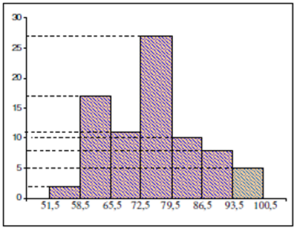
Histogram adalah sajian tabel distribusi frekuensi dengan menggunakan gambar berbentuk pesegi panjang yang saling berhimpit.

Langkah-langkah membuat histogram:

1.     Membuat sumbu datar dan sumbu tegak yang saling berpotongan. Sumbu datar menyatakan kelas interval dan sumbu tegak menyatakan frekuensi

2.    Buat skala menggunakan batas-batas kelas interval

3.    Bentuk batang sesuai dengan batas kelas interval dan frekuensi. Sisi-sisi dari batang kelas interval harus berdekatan dan berhimpit

Contoh:
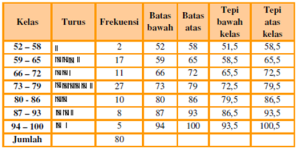
Data nilai ulangan matematika dari 80 siswa SMP Tunas Hijau Sidoarjo yang telah disajikan dalam tabel distribusi frekuensi.

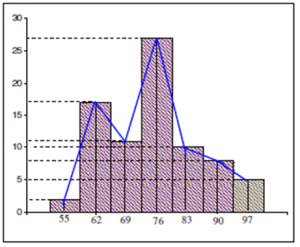
Poligon adalah diagram garis yang dibentuk dengan cara menghubungkan titik tengah bagian sisi atas persegi panjang pada histogram.

Langkah-langkah membuat poligon:

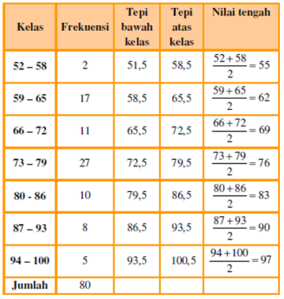
4.    Buat titik tengah kelas: (nilai ujung bawah + nilai ujung atas) x ½

5.    Buat tebel distribusi frekuensi mutlak dengan kolom tambahan berupa kolom titik tengah kelas

6.    Buat grafik poligon dengan melihat data pada tabel distribusi frekuensi mutlak

Contoh:
Data nilai ulangan matematika dari 80 siswa SMP Tunas Hijau Sidoarjo yang telah disajikan dalam tabel distribusi frekuensi.

Untuk mempelajari langkah-langkah penyajian data dengan menggunakan diagram lingkaran (pie)  kalian bisa langsung mengamati contoh soal yang ada di bawah ini:

Contoh Soal:

Di dalam sebuah kelas terdapat siswa sebanyak 60 orang. Masing-masing siswa diwajibkan untuk memiliki setidaknya satu jenis kegiatan ekstrakulikuler. Setelah dikumpulkan, diperoleh data yaitu 15 orang siswa memilih basket, 17 siswa memilih bola voli, 24 siswa memilih futsal, dan 4 orang memilih Pramuka. Buatlah diagram ,ingkaran dari data tersebut!

Penyelesaian:

Sebelum membat diagram lingkaran dari data tersebut, kita harus mencari persentasenya terlebih dahulu sehingga nantinya kita bisa menentukan besarnya sudut dari masing-masing data yang diperoleh.

Setelah kita peroleh persentase dan besar sudutnya, kita bisa menyajikan data tersebut ke dalam diagram lingkaran seperti di bawah ini:

Demikianlah ulasan dan rangkuman materi tentang cara Penyajian Data Menggunakan Diagram Lingkaran semoga pembahasan contoh soal di atas bisa membuat kalan paham tentang langkah-langkah yang harus dilakukan ketika ingin menyajikan data dalam bentuk diagram lingkaran dimana data-data yang diperoleh digambarkan dalam bentuk persentase dan besar sudut di salam sebuah lingkaran.

Pengertian Statistik

Statistik dalam arti sempit adalah mendeskripsikan atau menggambarkan mengenai data yang disajikan dalam bentuk

• Tabel dan diagram,
• Pengukuran tendensi sentral (rata-rata hitung, rata-rata ukur, dan rata-rata harmonik),
• Pengukuran penempatan (median, kuartil, desil, dan persentil),
• Pengukuran penyimpanan (range, rentangan antar kuartil, rentangan semi antar kuartil, simpangan rata-rata, simpangan baku, variasi, koefisien variansi dan angka baku), dan
• Angka indeks.

Sedangkan Statistika adalah suatu metode atau ilmu yang mempelajari cara pengumpulan, pengolahan, penganalisaan, penafsiran, dan penarikan kesimpulan dari data yang ada. Statistik dalam arti luas adalah suatu alat untuk mengumpulkan data, mengolah data, menarik kesimpulan, membuat tindakan berdasarkan analisis data yang dikumpulkan atau statistika yang digunakan menganalisis data sampel dan hasilnya dimanfaatkan untuk generalisasi pada populasi.

Dari kesimpulan di atas dapat ditarik kesimpulan bahwa statistika adalah ilmu yang mempelajari tentang seluk beluk data, yaitu tentang pengumpulan, pengolahan/analisis, penafsiran, dan penarikan kesimpulan dari data yang berbentuk angka-angka. Statistika banyak diterapkan dalam berbagai disiplin ilmu, baik ilmu-ilmu alam (misalnya astronomi dan biologi maupun ilmu-ilmu sosial (termasuk sosiologi dan psikologi), maupun di bidang bisnis, ekonomi, dan industri). Statistika juga digunakan dalam pemerintahan untuk berbagai macam tujuan; sensus penduduk merupakan salah satu prosedur yang paling dikenal. Aplikasi statistika lainnya yang sekarang popular adalah prosedur jajak pendapat atau polling (misalnya dilakukan sebelum pemilihan umum), serta jajak cepat (perhitungan cepat hasil pemilu) atau quick count. Di bidang komputasi, statistika dapat pula diterapkan dalam pengenalan pola maupun kecerdasan buatan.

Konsep Dasar

Dalam mengaplikasikan statistika terhadap permasalahan sains, industri, atau sosial, pertama-tama dimulai dari mempelajari populasi. Makna populasi dalam statistika dapat berarti populasi benda hidup, benda mati, ataupun benda abstrak. Populasi juga dapat berupa pengukuran sebuah proses dalam waktu yang berbeda-beda, yakni dikenal dengan istilah deret waktu.
Melakukan pendataan (pengumpulan data) seluruh populasi dinamakan sensus. Sebuah sensus tentu memerlukan waktu dan biaya yang tinggi. Untuk itu, dalam statistika seringkali dilakukan pengambilan sample (sampling), yakni sebagian kecil dari populasi, yang dapat mewakili seluruh populasi. Analisis data dari sampel nantinya digunakan untuk menggeneralisasikan seluruh populasi. Jika sampel yang diambil cukup representatif, inferensial (pengambilan keputusan) dan simpulan yang dibuat dari sampel dapat digunakan untuk menggambarkan populasi secara keseluruhan. Metode statistika tentang bagaimana cara mengambil sample yang tepat dinamakan teknik sampling.
Analisis statistik banyak menggunakan probabilitas sebagai konsep dasarnya. Sedangkan matematika statistika merupakan cabang dari matematika terapan yang menggunakan teori probabilitas dan analisis matematis untuk mendapatkan dasar-dasar teori statistika.

Statistik perlu diketahui dan dipelajari karena statistik berperan sebagai alat bantu dalam hal-hal : 

•    Menjelaskan hubungan antara variabel-variabel 
•   Membuat rencana dan ramalan 
•   Mengatasi berbagai perubahan 
•     Membuat keputusan yang lebih baik

Hubungan Statistika dengan Psikologi

Dalam bidang psikologi, statistik dapat digunakan untuk memprediksi perkembangan atau dampak dari suatu perilaku tertentu. Dan melalui statistik seseorang dapat memprediksi apa yang akan terjadi, yakni dengan menganalisis hubungan peristiwa-peristiwa masa lalu dengan apa yang terjadi saat ini dalam masalah yang sama. Psikologi dan statistika adalah ilmu pasti abstrak dan nyata karna kedua ilmu itu mempunyai metode penyelesain yang benar-benar valid dan pasti kegunaannya sangatlah banyak dan bervariasi dalam kehidupan kita, pekerjaan kita, dan individual. Selain itu, statistika juga dapat digunakan untuk memprediksi perkembangan atau dampak dari suatu perilaku tertentu. Dan melalui statistika seseorang dapat memprediksi apa yang akan terjadi, yakni dengan menganalisis hubungan peristiwa-peristiwa masa lalu dengan apa yang terjadi saat ini dalam masalah yang sama.
Contoh :
Mengukur IQ seseorang. Untuk lebih dapat yang akurat kita harus mengukur orang tersebut misalnya melalui penelitian.
Jadi dengan adanya statistika di Psikologi, sangat membantu. Karena statistika itu dilihat sebagai hal yang realibilitas dan validitas.